اتحادها

فاکتورگیری و تجزیه

همانطور که اشاره شد، فاکتورگیری یک فرایند است که طی آن فاکتورهای یک عدد، یک چندجمله‌ای و یک عبارت مشخص می‌شود. در واقع فرایند یافتن فاکتورها و اجزایی که ضرب آن‌ها برابر با عبارت اولیه می‌شود را فاکتورگیری می‌نامند.

توجه کنید که به فرایند فاکتورگیری، تجزیه نیز می‌گویند زیرا طی آن، یک عبارت به صورت حاصل ضرب چند عبارت دیگر نوشته و تجزیه می‌شود. در ادامه، این مفهوم به کمک یک مثال مورد مطالعه قرار می‌گیرد.

مثال

عبارت زیر را تجزیه کنید یا به عبارت دیگر آن را به صورت حاصل ضرب عوامل سازنده‌اش بنویسید.

با دقت به رابطه بالا، متوجه می‌شویم که هر دو عبارت 2y و 6، شامل ضریب 2 هستند. در واقع 2y برابر با حاصل ضرب 2 در y است (y×2) و 6 را می‌توان به صورت 2×3 نوشت. بنابراین با توجه به نکته‌ای که بیان شد، از ضریب دو در رابطه فوق می‌توان فاکتورگیری کرد و رابطه بالا را به فرم زیر تجزیه کرد.

بنابراین 2y+6 شامل دو فاکتور 2 و y+3 است.

نکته مهم دیگری که باید به آن اشاره کرد این است که فاکتورگیری و تجزیه دقیقا مفهومی مقابل با گسترش و بسط دارند. مقایسه دو مفهوم گسترش و فاکتورگیری در شکل زیر به خوبی نشان داده شده است.

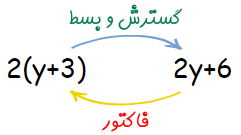
فاکتورهای رایج در مبحث اتحاد و تجزیه

در بخش قبل نشان داده شد که عدد 6 و عبارت 2y، یک فاکتور مشترک دارند که این فاکتور مشترک برابر با 2 است. برای آنکه عمل تجزیه و فاکتورگیری را به درستی و با صرف کمترین زمان انجام دهیم، لازم است که با تعداد زیادی از این فاکتورها آشنا باشیم که در این بخش، برخی از این فاکتورهای رایج را بیان می‌کنیم.

مثال

فرم تجزیه شده عبارت زیر را بنویسید.

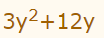
نکته بسیار مهمی که باید به آن اشاره کرد این است که دو عدد موجود در رابطه بالا یعنی 3 و 12، ضریبی از عدد 3 هستند. بنابراین یکی از فاکتورهای عبارت بالا، برابر با عدد 3 است که با استفاده از آن می‌توان رابطه موجود در صورت سوال را به فرم ساده شده زیر نمایش داد.

اما این رابطه را هنوز می‌توان به فرم ساده‌تری نوشت و آن را تجزیه کرد. با دقت به رابطه بالا می‌توان متوجه شد که عبارت y در هر دو عبارت y² و 4y مشترک است. بنابراین این رابطه را در نهایت می‌توان به شکل تجزیه شده زیر بیان کرد.

درستی عبارت تجزیه شده را می‌توان با استفاده از روند زیر مورد بررسی قرار داد.

در ادامه این مطلب، فرایند تجزیه و فاکتورگیری را برای روابط و چند جمله‌ای‌های پیچیده‌تری مورد بررسی قرار می‌دهیم.

تجزیه و فاکتورگیری از عبارات پیچیده

توجه کنید که عملیات تجزیه و فاکتورگیری یک رابطه، تنها شامل عبارات ساده مانند مثال‌های بخش قبل نیست و می‌تواند عملیات سخت و پیچیده‌ای را در بر بگیرد. دلیل پیچیدگی عملیات تجزیه و فاکتورگیری یک رابطه، این است که ما به دنبال عوامل و فاکتورهایی هستیم که با ضرب آن‌ها در یکدیگر، رابطه اولیه به دست می‌آید.

برای درک بهتر، ما به دنبال اجزای مختلف یک کیک هستیم که با بهم پیوستن آن‌ها، کیک خوشمزه تولید شده است. این موضوع را می‌توان به شکل زیر نمایش داد.

اما خبر خوب این است که هرچه تجربه و تمرین شما بیشتر باشد، فاکتورگیری کردن و تجزیه یک رابطه نیز برای شما راحت‌تر خواهد بود و با سرعت بیشتری روابط مختلف را تجزیه و فاکتورگیری می‌کنید. بنابراین برای تمرین بیشتر به مثال زیر توجه کنید.

مثال

عبارت زیر را تجزیه (فاکتورگیری) کنید.

همانطور که مشاهده می‌شود، عبارات رایج فاکتورگیری (وجود یک ضریب مشترک در هر دو بخش رابطه یعنی 4x² و 9) در این رابطه مشاهده نمی‌شوند. بنابراین ما نیاز به استفاده از سایر روابط موجود در ریاضیات داریم. در ریاضیات، رابطه اتحاد مزدوج را می‌توان به شکل زیر بیان کرد.

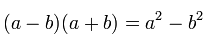
بنابراین رابطه ابتدای این مثال را طوری بازنویسی می‌کنیم که مشابه با رابطه بالا باشد. این موضوع در رابطه زیر به خوبی نشان داده شده است.

در واقع عبارت $$4x^2$$ را می‌توان به فرم $$(2x{)}^2$$ نوشت. همچنین می‌دانیم که عدد ۹ برابر با 3² است. بنابراین رابطه صورت سوال به شکل زیر در می‌آید.

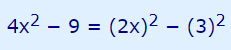
در ادامه رابطه فوق را به شکل اتحاد مزدوج بازنویسی می‌کنیم. مقدار a و b در رابطه اتحاد مزدوج به ترتیب برابر با 2x و 3 است. بنابراین با قرار دادن این دو مقدار در رابطه اتحاد مزدوج، رابطه زیر به دست می‌آید.

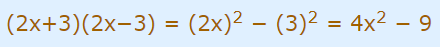
همانطور که مشاهده می‌شود فاکتورهای عبارت صورت سوال (رابطه $$4x^2–9$$)، برابر با $$(2x+3)$$ و $$(2x-3)$$ هستند. بنابراین پاسخ مسئله به شکل زیر بیان می‌شود.

در واقع برای فاکتورگیری و محاسبه تجزیه یک عبارت، باید تمرین بسیار زیاد کنیم و با فرمول‌های انواع اتحاد نیز آشنایی داشته باشیم. در واقع با بیان انواع اتحاد‌ها شما با مبحث اتحاد و تجزیه به صورت کامل آشنا خواهید شد. در ادامه این اتحادها به صورت دقیق مورد بررسی قرار می‌گیرد.

انواع اتحادها

در ادامه لیستی از اتحادهای رایج در ریاضیات بیان می‌شوند. با استفاده از این اتحاد‌ها می‌توان تجزیه عبارات مختلف را به خوبی انجام داد. توجه کنید که مبحث اتحاد و تجزیه کاربرد بسیار زیادی در تجزیه کسرها و محاسبه انتگرال به کمک کسرهای جزئی نیز دارد.

نکته دیگری که می‌توان به آن اشاره کرد این است که با استفاده از این اتحاد‌ها، بسیاری از معادلات مختلف در ریاضیات را می‌توانیم به شکل راحت‌تری مورد مطالعه قرار دهیم. در واقع پاسخ یک معادله به کمک اتحادهای زیر به سرعت قابل محاسبه است.

اتحاد مربع دو جمله‌ای

این اتحاد را می‌توان به عنوان شکل دیگری از معادله درجه دو بیان کرد. در واقع عبارت $$(a-b{)}^2$$ را می‌توان به صورت حاصل ضرب $$(a-b)$$ در خودش نوشت. بنابراین اتحاد مربع دو جمله‌ای زمانی که $$(a-b{)}^2$$ و $$(a+b{)}^2$$ داشته باشیم را می‌توان به شکل زیر بیان کرد.

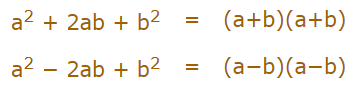
اتحاد مربع سه جمله‌ای

اتحاد مربع دو جمله‌ای، حالتی را نشان می‌داد که مجموع یا تفاضل دو جمله a و b، به توان دو رسیده باشند. بنابراین به صورت مشابه می‌توان اتحاد مربع سه جمله‌ای را مورد بررسی قرار داد. اتحاد مربع سه جمله‌ای، حالتی را نشان می‌دهد که مجموع سه جمله b ،a و c به توان دو رسیده باشد. فرمول این اتحاد در رابطه زیر نشان داده شده است.

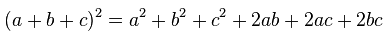
توجه کنید که حالت منفی عبارت فوق یعنی ²(a+b-c) کاربرد زیادی در مسائل ندارد ولی پیشنهاد می‌شود، این عبارت یعنی ²(a+b-c) را به عنوان تمرین محاسبه کنید.

اتحاد مکعب دو جمله‌ای

اتحاد پرکاربرد دیگر در ریاضیات، اتحاد مکعب دو جمله‌ای است. این اتحاد، مجموع یا تفاضل دو عبارت a و b را به توان سه می‌رساند. کاربرد زیاد این اتحاد در مباحث مرتبط با اتحاد و تجزیه باعث شده است که بتوانیم آن را به شکل زیر و به عنوان یکی از اتحادهای رایج بیان کنیم.

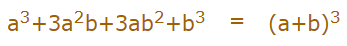
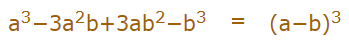
توجه کنید که به رابطه اول، مکعب مجموع دو جمله‌ای و به رابطه دوم مکعب تفاضل دو جمله‌ای نیز می‌گویند.

اتحاد چاق و لاغر

اتحاد چاق و لاغر از یک جمله کوچک (لاغر) و یک جمله بزرگ (چاق) تشکیل شده است. برای نوشتن این اتحاد، لازم است که به علامت عبارات مختلف دقت کنید. این موضوع در رابطه زیر به خوبی نشان داده شده است.

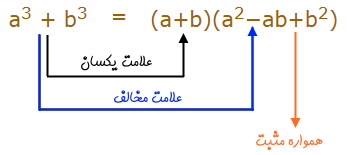
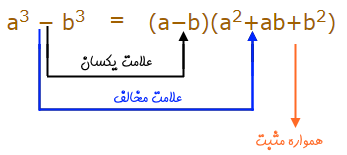
بنابراین برای نوشتن رابطه اتحاد چاق و لاغر به علامت‌های نشان داده شده در شکل‌های بالا به خوبی توجه کنید. نکته دیگر این است که این اتحاد را مجموع و تفاضل مکعبات دو جمله نیز می‌نامند.

اتحاد مزدوج

یکی از پرکاربردترین اتحادها است. فرمول این اتحاد را می‌توان به شکل زیر بیان کرد.

نکته:اتحاد مزدوج را همان اتحاد دوم نیز میتوان در نظر گرفت.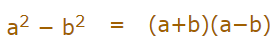

اتحاد جمله مشترک

اتحاد جمله مشترک یکی دیگر از اتحادهایی است که با دانستن آن، می‌توانید حاصل ضرب دو عبارت را به خوبی پیدا کنید و یا یک دو جمله‌ای را به راحتی به عوامل سازنده‌اش تجزیه کنید. این اتحاد و تجزیه صورت گرفته به وسیله آن، کاربرد زیادی در تجزیه کسرها، حل معادلات و همچنین محاسبه انتگرال دارد و رابطه آن را می‌توان به شکل زیر بیان کرد.

اتحاد بسط دو جمله‌ای نیوتن

در قسمت قبل، اتحاد مربع و مکعب دو جمله‌ای بیان شد. این حالت را می‌توان برای توان n نیز تعمیم داد که به آن بسط دو جمله‌ای نیوتن گفته می‌شود. بسط دو جمله‌ای نیوتن را می‌توان برای مجموع دو جمله و تفاضل دو جمله، به شکل زیر نمایش داد.

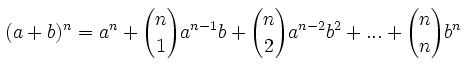
برای نوشتن عبارت بالا به دو نکته توجه کنید. نکته اول علامت‌های موجود در دو رابطه بالا است و نکته دوم این است که مجموع توان a و b در هرکدام از جملات موجود در روابط بالا برابر با n است.

اتحاد لاگرانژ

اتحاد لاگرانژ برای حالتی کاربرد دارد که با چهار متغیر سر و کار داریم. این چهار متغیر را می‌توان با نمادهای x ،b ،a و y نمایش داد.

نکته بسیار مهم دیگری که باید به آن توجه کرد این است که به جای هرکدام از چهار متغیر بالا ممکن است یک عدد قرار گرفته باشد. بنابراین باز هم می‌توان رابطه بالا را برای آن‌ها نوشت و تنها به جای متغیر نشان داده شده، عدد آن را قرار می‌دهیم.

اتحاد اویلر

اتحاد اویلر را می‌توان به شکل زیر بیان کرد.

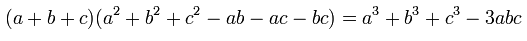
توجه کنید که اتحاد اویلر را می‌توان به شکل دیگری هم نمایش داد که در رابطه زیر نشان داده شده است.

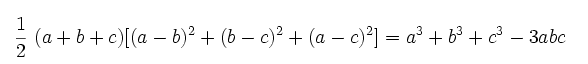
حالات خاص اتحاد اویلر بسیار پرکاربرد است. یکی از حالات خاص این اتحاد، زمانی است که مجموع سه متغیر b ،a و c برابر با صفر باشد. بنابراین اگر $$a+b+c=0$$ باشد، داریم:

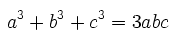
این رابطه با توجه به رابطه اول اویلر به دست آمده است. رابطه دیگری را نیز برای حالتی که سه متغیر b ،a و c با یکدیگر برابر باشند می‌توان بیان کرد. بنابراین با استفاده از رابطه دوم اویلر می‌توان نتیجه گرفت که اگر $$a=b=c$$ باشد، رابطه زیر برقرار است.

توصیه ما این است که روابط بیان شده را با ضرب عبارات داخل پرانتز محاسبه کنید و بارها و بارها اثبات آن را روی کاغذ برای خود بنویسید. نکته دیگری که باید به آن توجه کنید این است که به خاطر سپردن روابط بالا، تنها از طریق حل کردن مثال‌های متعدد توصیه می‌شود و اگر تنها خود فرمول را حفظ کنید، دردی از شما دوا نمی‌شود.

بنابراین برای استفاده از روش‌های اتحاد و تجزیه و همچنین حل مسائل مختلف، سه مرحله زیر را برای تجزیه روابط گوناگون رعایت کنید.

• مرحله اول این است که از روش‌های بیان شده در بخش فاکتورهای رایج استفاده کنید و عبارت داده شده را تا جای ممکن به صورت ساده بنویسید.
• مرحله دوم این است که به فرمول اتحادهای مختلف توجه کنید و ببینید آیا می‌توانید رابطه به دست آمده از مرحله اول را به کمک اتحادها به فرم ساده‌تری بنویسید یا خیر.
• در انتها و مرحله سوم، باید مرحله دوم را بارها و بارها تکرار کنید تا بتوانید تمام فاکتورهای رابطه صورت سوال را به صورت کامل به دست آورید.

مثال‌ها

همانطور که اشاره شد، برای تسلط بر مبحث اتحاد و تجزیه باید مثال‌های متعددی را حل کنید. بنابراین در این بخش، چند مثال برای یادگیری کاربرد مفاهیم ذکر شده، آورده شده است.

مثال 1

عبارت زیر را تجزیه کنید.

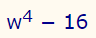
همانطور که مشاهده می‌شود، در عبارت اول این رابطه، توان چهارم حضور دارد، بنابراین احتمالا می‌توان کل رابطه را به شکل توان دو نیز بیان کرد. این موضوع در رابطه زیر نشان داده شده است.

همانطور که مشاهده می‌شود، رابطه بالا مشابه با اتحاد مزدوج است. بنابراین آن را به فرم تجزیه و فاکتورگیری شده زیر بیان می‌کنیم.

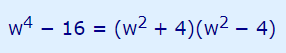
با دقت به رابطه بالا متوجه می‌شویم که عبارت دوم در سمت راست معادله بالا نیز اتحاد مزدوج را نشان می‌دهد و می‌توان آن را ساده کرد. بنابراین با استفاده مجدد از این اتحاد و تجزیه عبارت فوق، رابطه بالا به شکل زیر در می‌آید.

مثال 2

رابطه زیر را با استفاده از روابط ارائه شده در مبحث اتحاد و تجزیه به صورت حاصل ضرب عوامل سازنده‌اش بنویسید.

در ابتدا و با استفاده از روش ذکر شده در بخش فاکتورهای رایج، متوجه می‌شویم که عبارت 3u در هر دو بخش رابطه بالا وجود دارد. بنابراین می‌توانیم از این عبارت به شکل زیر فاکتور بگیریم.

در ادامه با استفاده از اتحاد چاق و لاغر، رابطه $$u^3–8v^3$$ موجود در رابطه بالا را به فرم ضرب دو عبارت می‌نویسیم. این موضوع در رابطه زیر نشان داده شده است.

مثال 3

رابطه زیر را تجزیه کنید.

در ابتدا با استفاده از فاکتورگیری، رابطه بالا را ساده می‌کنیم. همانطور که مشاهده می‌شود عبارت $$z^2$$ در دو عبارت اول مشترک است و عدد 9 نیز در دو عبارت آخر مشاهده می‌شود. بنابراین رابطه فوق را می‌توان به شکل ساده شده زیر بیان کرد.

در رابطه بالا عبارت (z-1) بین هر دو عبارت مشترک است، بنابراین می‌توان رابطه بالا را به شکل ساده شده زیر بیان کرد.

همانطور که مشاهده می‌شود با استفاده از روندی که طی شد، رابطه صورت سوال به صورت ضرب دو عبارت نوشته شده است ولی همچنان این رابطه را می‌توان به شکل ساده‌تری نیز بیان کرد. با دقت به رابطه بالا متوجه می‌شویم که عبارت اول، فرمول اتحاد مزدوج را نشان می‌دهد. بنابراین داریم:

بنابراین با استفاده از فاکتورگیری‌های رایج و استفاده از اتحاد‌های گوناکون می‌توان روابط مختلف را به صورت حاصل ضرب چند عبارت در یکدیگر بیان کرد.




پایان.
منبع: مجله فرادرس
منبع: دانشلند